堆数据结构定义
堆是一个完全二叉树，通常使用数组来表示，其中树中的每个节点都具有一个值。
如下图所示：
这意味着树中的所有层次除了最底层都是完全填充的，而且最底层的节点从左到右填充。
堆数据结构作用
堆数据结构主要用于以下几方面：
1.实现优先队列
堆可用于实现高效的优先队列，其中元素具有优先级，并且具有最高或最低优先级的元素可以快速访问。
2.堆排序
堆排序是一种高效的排序算法，利用堆来对元素进行排序。
3.图算法
在图算法中，堆经常用于Dijkstra算法和Prim算法等，以找到最短路径和最小生成树。
4.内存分配
堆内存通常用于动态分配和管理对象，如Java中的对象分配。
5.任务调度
在操作系统和并发编程中，堆可用于实现任务调度和线程管理。
堆数据结构实现
堆有两种主要类型：最大堆和最小堆。
最大堆（Max Heap）
在最大堆中，父节点的值始终大于，或等于其子节点的值。
如下图所示：
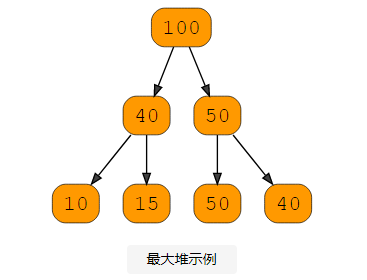
最大堆中的元素遵循最大堆属性，这意味着父节点的键始终大于两个子节点的键。
要构建最大堆：
- 在堆的开头（根）创建一个新节点，为其指定一个值。
- 将子节点的值，与父节点的值进行比较。
- 如果父节点的值，小于任一子节点的值（向左或向右），则交换节点。
- 重复此操作，直到最大元素位于根父节点，此时可以说堆属性成立。
最大堆通常用于实现优先队列，其中具有最高优先级的元素位于堆的顶部。
最小堆（Min Heap）
在最小堆中，父节点的值，始终小于或等于其子节点的值。
直观上，我们可以说最小堆中的元素遵循最小堆属性，因为这与最大堆相反。
最小堆通常用于实现优先队列，其中具有最低优先级的元素位于堆的顶部。
堆的实现
堆通常使用数组来表示，其中树的节点按特定顺序存储在数组中。
堆的根节点存储在数组的第一个元素（索引为0或1，具体取决于实现）。
对于节点i，其左子节点存储在索引2i+1，右子节点存储在索引2i+2。
堆中的元素必须满足堆的性质，即最大堆或最小堆。
在实现堆时，需要提供一组操作，如：插入、删除、上浮和下沉操作，以确保堆的性质得以维护。
堆的基本操作
插入（Insertion）
将新元素插入堆，并确保堆的性质得以保持。通常是将新元素添加到数组的末尾，然后进行一系列”上浮”操作。
删除最大/最小元素（Extract Max/Min）
从堆中移除根节点（最大堆中为最大元素，最小堆中为最小元素），然后通过将最后一个元素移到根位置，进行一系列”下沉”操作，以维护堆的性质。
堆数据结构使用
在Java中，你可以使用内置的PriorityQueue类来轻松创建堆。
import java.util.PriorityQueue; // 创建最小堆 PriorityQueue<Integer> minHeap = new PriorityQueue<>(); // 插入元素 minHeap.offer(5); minHeap.offer(2); minHeap.offer(8); // 获取最小值 int min = minHeap.poll(); // 最小值是2 // 创建最大堆 PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Collections.reverseOrder()); // 插入元素 maxHeap.offer(5); maxHeap.offer(2); maxHeap.offer(8); // 获取最大值 int max = maxHeap.poll(); // 最大值是8
堆的实现原理在算法和数据结构中非常重要，它可以用于高效地解决各种问题，如优先队列、堆排序、图算法和任务调度等。
堆数据结构总结
堆是一种高效的数据结构，用于处理具有优先级的数据，同时也用于解决一些基本的算法问题。
堆排序是一种稳定的排序算法，时间复杂度为O(n log n)，在某些情况下，堆可以在实际应用中发挥巨大的作用。
mikechen
mikechen睿哥，10年+大厂架构经验，资深技术专家，就职于阿里巴巴、淘宝、百度等一线互联网大厂。
关注「mikechen」公众号，获取更多技术干货！
后台回复【架构】即可获取《阿里架构师进阶专题全部合集》，后台回复【面试】即可获取《史上最全阿里Java面试题总结》